OSSD课程之帕斯卡三角形
2020-05-22 环球教育
今天给大家分享OSSD之帕斯卡三角形,大家都熟知我们古代的科举制度是封建社会选举人才最重要的方式,主要涉及到政治和语文,难道我们在古代就只学这两门吗?当然不是,其实中国是世界文明古国之一。数学是中国古代科学中一门重要学科,其发展源远流长,成就辉煌。根据它本身的,可以分为五个时期:(1)先秦萌芽时期;(2)汉唐奠基时期;(3)宋元全盛时期;(4)西学输入时期;(5)近现代数学发展时期。
唐代以来一些数学著作的失传,大概是五代十国分裂战乱所造成的文化后果。到了宋代,雕版印数的发达特别是活字印刷的发明,则给数学著作的保存与流传带来了福音。事实上,整个宋元时期(公元960-1368),重新统一了的中国封建社会发生了一系列有利于数学发展的变化。商业的繁荣、手工业的兴盛以及由此引起的技术进步(四大发明中有三项—指南针、火药和活字印刷是在宋代完成并获得广泛应用),给数学的发展带来新的活力。这一时期涌现的优秀数学家中最卓越的代表,如通常称“宋元四大家”的杨辉、秦九韶、李治、朱世杰等,在世界数学史上占有光辉的地位;而这一时期印刷出版、记载着中国古典数学最高成就的宋元算书,也是世界文化的重要遗产。北宋人贾宪约1050年首先使用“贾宪三角”进行高次开方运算,他的主要贡献是创造了”贾宪三角’和增乘开方法,增乘开方法即求高次幂的正根法。南宋数学家杨辉在《详解九章算法》(1261年)记载并保存了“贾宪三角”,故称杨辉三角。元朝数学家朱世杰在《四元玉鉴》(1303年)扩充了“贾宪三角”成“古法七乘方图”(如下图)。在欧洲直到1623年以后,法国数学家帕斯卡在13岁时发现了“帕斯卡三角”。
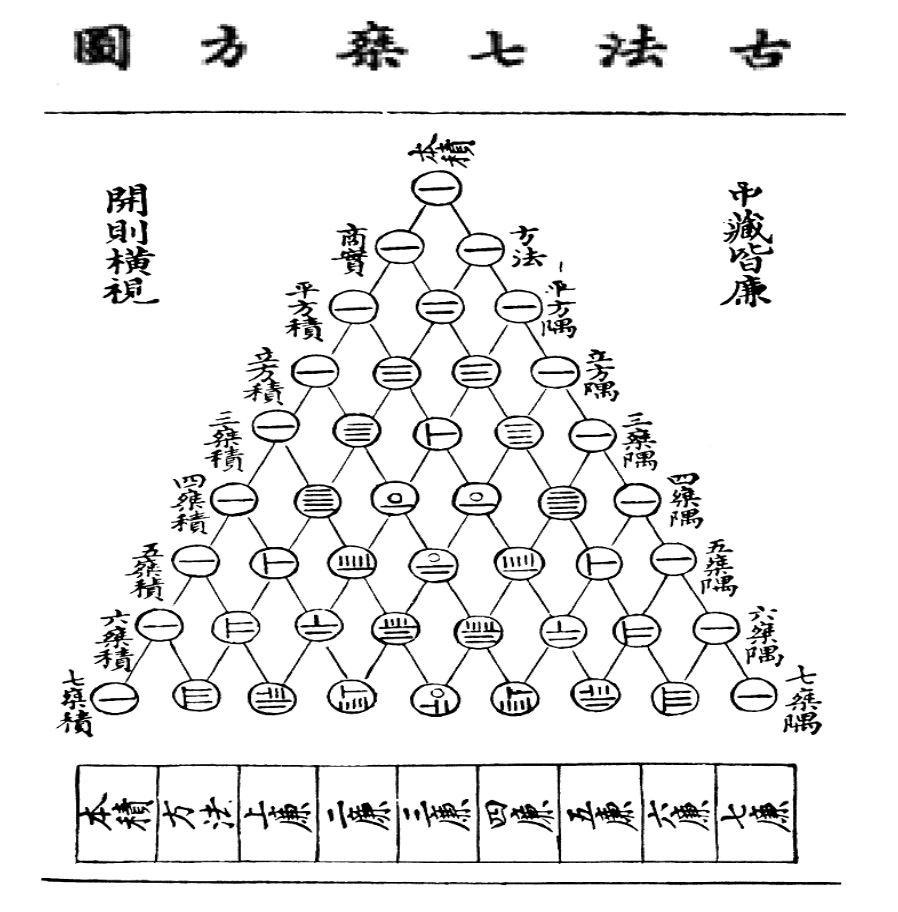
在OSSD的MDM4U这门学科当中,我们也学习到了这个知识点,我们就学习到了这个知识点,并且用比较简单易懂的方法总结了另外的形式就如下图

我们会发现一些规律,难易都有。
1.每个数等于它上方两数之和。
2.每行数字左右对称,由1开始逐渐变大。
3.第n行的数字有n项。
4.前n行共[(1+n)n]/2个数。
5.第n行的m个数可表示为 C(n-1,m-1),即为从n-1个不同元素中取m-1个元素的组合数。
6.第n行的第m个数和第n-m+1个数相等,为组合数性质之一。
7.每个数字等于上一行的左右两个数字之和。可用此性质写出整个杨辉三角。即第n+1行的第i个数等于第n行的第i-1个数和第i个数之和,这也是组合数的性质之一。即 C(n+1,i)=C(n,i)+C(n,i-1)。
8.(a+b)n的展开式中的各项系数依次对应杨辉三角的第(n+1)行中的每一项。
9.将第2n+1行第1个数,跟第2n+2行第3个数、第2n+3行第5个数……连成一线,这些数的和是第4n+1个斐波那契数;将第2n行第2个数(n>1),跟第2n-1行第4个数、第2n-2行第6个数……这些数之和是第4n-2个斐波那契数。
10.将第n行的数字分别乘以10^(m-1),其中m为该数所在的列,再将各项相加的和为11^(n-1)。11^0=1,11^1=1x10^0+1×10^1=11,11^2=1×10^0+2x10^1+1x10^2=121,11^3=1x10^0+3×10^1+3x10^2+1x10^3=1331,11^4=1x10^0+4x10^1+6x10^2+4x10^3+1x10^4=14641,11^5=1x10^0+5x10^1+10x10^2+10x10^3+5x10^4+1×10^5=161051。
11.第n行数字的和为2^(n-1)。1=2^(1-1),1+1=2^(2-1),1+2+1=2^(3-1),1+3+3+1=2^(4-1),1+4+6+4+1=2^(5-1),1+5+10+10+5+1=2^(6-1)。
12.斜线上数字的和等于其向左(从左上方到右下方的斜线)或向右拐弯(从右上方到左下方的斜线),拐角上的数字。1+1=2,1+1+1=3,1+1+1+1=4,1+2=3,1+2+3=6,1+2+3+4=10,1+3=4,1+3+6=10,1+4=5。
13.将各行数字左对齐,其右上到左下对角线数字的和等于斐波那契数列的数字。1,1,1+1=2,2+1=3,1+3+1=5,3+4+1=8,1+6+5+1=13,4+10+6+1=21,1+10+15+7+1=34,5+20+21+8+1=55。
其实总结了这些规律,我在想,如果当初的宋朝像如今这样信息发达,会不会在欧洲所有人都会叫它杨辉三角而不是帕斯卡三角形了呢?
下面给大家留了一个小练习,不知道你能否用刚刚学过的知识解决出来呢?

下期揭晓答案呦~886


1 秋季雅思培训班全面解析:多元课程体系+精准提分策略,助你高效冲刺目标分数
2 秋季雅思培训班全面开课:分层教学适配多元需求,抢占备考黄金期
3 秋季雅思 4 分培训班报名开启:夯实基础,轻松拿下入门目标分
4 秋季雅思6.5分冲刺攻略:课程选择与高分策略全解析
5 雅思秋季班报名启动:封闭集训、OMO混合课程成新趋势
6 出国雅思培训班:为留学之路筑牢语言基石
7 雅思备考进入「精准提分」时代:从痛点到破局,2025年考生需要怎样的培训?
8 雅思课程培训:体系化学习,高效突破分数壁垒
9 2025雅思培训班避坑指南:如何选择高性价比机构?
10 2025雅思口语培训新生态:动态题库下的高分突围指南
北京市海淀区环球雅思培训学校 版权所有 课程咨询热线:400-616-8800
Copyright 1997 – 2025 gedu.org. All Rights Reserved 京ICP备10036718号
全部课程、服务及教材面向18岁以上人群
市场合作申请