OSSD反函数的概念
2020-05-27 环球教育
大家好,今天我们来聊一下OSSD反函数的概念。
Inverse functions are a special class of functions that undo each other. The input and output values for two inverse functions, f(x) = 2x + 1 and g(x) = x-12 , are shown below:
反函数是一类相互撤销的特殊函数。两个反函数的输入和输出值如下所示:
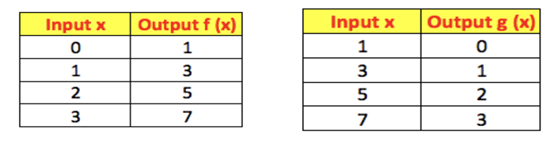
Notice that the output of the first function, f(x), becomes the input for the second function, g(x). The function g(x) undoes what f(x) does. The ordered pairs of g(x) can be found by switching the coordinates in each ordered pair of f(x).
Recall that a relation is a set of ordered pairs. The inverse of a relation can be found by interchanging the domain and the range of the relation:
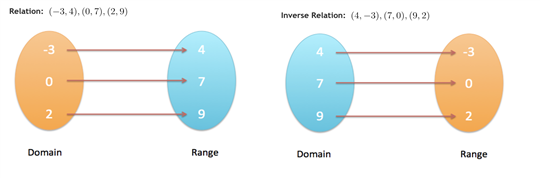
请注意,第一个函数f(x)的输出成为第二个函数g(x)的输入。
回想一下,关系是一组有序对。反函数关系可通过互换关系的域和范围来找到。
You will also recall that a function is a special relation. For each element in the domain of a function, there is exactly one element in the range. If the inverse of a function f(x), is also a function, it is called the inverse function of f(x). The inverse function is represented by f-1(x).
The notation of f-1 is read as 'the inverse of f' or simply 'f inverse'. Please note that -1 is not an exponent(指数), therefore, f-1≠ 1f
The table shows ordered pairs belonging to a function f(x). Determine f-1(x), graph f(x) and its inverse and state the domain and range of f(x) and its inverse.
下表显示了属于函数f(x)的有序对。接下来我们确定 f-1(x),图及其逆,并说明其逆的定义域和值域。
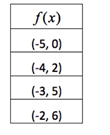
In this example, switch the x and y coordinates, and then plot the points.
在此示例中,切换x和y坐标,然后绘制点

Notice that switching the x and y coordinates reflects the graph of f(x) in the line y = x.
请注意,切换和坐标会转换直线中的x与y关系
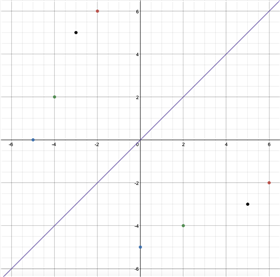
Notice below that the domain of f(x) is the range of f-1(x) , and the range of f(x) is the domain of f-1(x) :
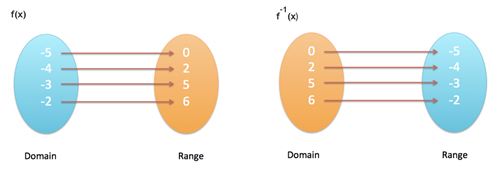
请注意,上图中f(x)的定义域是f-1(x) 的值域,f(x)的值域是f-1(x) 的定义域。这就是求f(x)反函数的方法。
更多OSSD知识可以持续关注http://beijing.gedu.org


1 环球教育培训学校2025寒假雅思课程全面升级,助力突破语言瓶颈
2 环球教育三维动态教学体系精准应对雅思改革,2025寒假班助力考生冲刺高分
3 环球教育雅思培训:三维动态教学体系引领留学备考新风尚
4 环球教育多维创新引领语言培训,28年深耕构建国际教育生态圈
5 环球教育培训机构 2025 年度成果发布,全品类服务覆盖学子成长全周期
6 环球教育雅思班全新升级,三维动态教学体系精准应对机考改革
7 环球学校雅思培训:三维动态教学体系助力学子精准提分
8 雅思6分相当于英语几级?国内英语等级对照全解析
9 环球教育雅思培训再添高分案例,28 年深耕铸就提分标杆
10 环球教育培训学校:以多元课程与匠心服务,点亮学子成长之路
北京市海淀区环球雅思培训学校 版权所有 课程咨询热线:400-616-8800
Copyright 1997 – 2025 gedu.org. All Rights Reserved 京ICP备10036718号
全部课程、服务及教材面向18岁以上人群
市场合作申请